Sugar Bad, Fiber Great: How to Use ChatGPT to Analyze Diet’s Impact on Weight
Introduction
For almost two and a half years, I have recorded my diet, weight, and exercise data in MyFitnessPal. I recently decided to use ChatGPT’s Data Analyst to analyze my diet’s impact on weight. This analysis supplements my growing understanding of my personal metabolic dynamics. The results all at once surprised me, confirmed intuitions, and pointed to the need for future analysis. I also learned some important lessons about how to interface with ChatGPT’s Data Analyst.
At a high level, the Data Analyst concluded the following about my diet’s impact on weight:
- Fiber has the largest impact on my weight and tends to drive weight loss. No other nutrient even comes close to fiber’s impact. This result greatly surprised me.
- Protein has the second largest impact on my weight and tends to drive weight gain (I assume, perhaps optimistically, that at least part of this weight gain comes from muscle through weightlifting)
- Fat has the third largest impact and … 🥁🥁🥁 is associated with weight loss. The adage “fat doesn’t make you fat” rings true for me. I speculate that fats satiate hunger better than sugar. However, the calorie “crowding out” is very subtle and requires deeper analysis to understand.
- Sugar has the fourth largest impact and tends to drive weight gain. I am not surprised by the impact, but I assumed sugar would have the largest absolute impact on my weight.
- Net carbohydrates (excluding sugar and fiber) has a near zero impact on my weight.
I ran numerous trials and prompts to get to the results presented below. Fortunately, each run produced consistent conclusions. The iterations produced better visualizations and improved descriptions of the analysis. I had to coax ChatGPT on non-linear models, including pointing out the need for cross-validation to prevent over-fitting. In the final iteration below, ChatGPT stuck with Random Forest as its non-linear model whereas in previous iterations it examined Gradient Boost and Support Vector Regressors (both performed worse than Random Forest). I expected Data Analyst to do more rigorous examination of the linear regression’s results. For example, the R² and MSE values are sufficient for my purposes, but the Data Analyst only provided relative commentary on the robustness of these fits.
I also ran into a few bugs where the Data Analyst failed to produce visualizations or even failed to analyze the data. In the most catastrophic incidences, I put the work on the shelf and returned another day. Text in curly brackets represent my commentary.
Impact of Nutrients on (Personal) Weight
The prompt below describes the research objective and approach.
The Research Question: The ChatGPT Prompt
I have attached a daily time series of data measuring weight, net carbohydrates, sugar, fat, fiber, and protein. I want you to build models that explain the relationship of these measures where weight is the dependent variable and the other measures are independent variables. Ignore the carbohydrates (g) column. Net carbohydrates excludes sugar and fiber. Also remember that nutrition’s impact on weight can take more than a day and can vary due to a variety of factors. Thus, I need to examine the results of several lagged models. Moreover, I did not measure weight every day. Many of the weight measures in the data are interpolated by repeating the last daily value in order to fill gaps. Here are the lags to use in model building:
- Model 1: 7-Day total for each nutrient versus subsequent 7-day average weight
- Model 2: 7-Day total for each nutrient versus subsequent 14-day average weight
- Model 3: 7-Day total for each nutrient versus 7-day average weight starting 7 days later
- Model 4: 1-Day total for each nutrient versus weight the next day (used as a comparison to understand the improvement from lagged models 1 through 3)
Provide recommendations on the best model(s) to use and provide detailed justifications. Include linear and non-linear models. Where needed, use validation on the non-linear models to avoid over-fitting. The best model is the model that has the most reliable and robust predictive power for weight based on nutritional intake. Provide visualizations for all models and results so that I can see the impact of each nutrient on weight.
Provide a summary of the impact of each individual nutrient on weight by quantifying the coefficients from the models. Use a summary table with one column per model and each row has a nutrient or measures of model accuracy or fit.
The Results: ChatGPT’s Response
The following response from ChatGPT is slightly edited for clarity. I left most of the response intact to demonstrate the fluidity of ChatGPT’s presentation. The Appendix at the end of this post describes the technical concepts (produced of course by ChatGPT). Note well that these results are presented for informational purposes and do not represent health advice.
Data Preparation
- Exclude Carbohydrates Column: As per your instructions, we’ll exclude the “Carbohydrates (g)” column.
- Date Parsing: Convert the “Date” column to datetime format.
- Lagging and Averaging: Create lagged features and averages as specified for models 1 through 4.
- Linear and Non-linear Models: Fit both types of models and evaluate their performance.
- Summary Table: Summarize the results including coefficients and measures of model fit.
Let’s proceed with these steps.
Step 1: Data Preparation
We’ll begin by preparing the dataset, computing the lagged features, and creating the necessary averages for the different models.
Step 2: Feature Engineering
- Model 1: 7-Day total for each nutrient vs. subsequent 7-day average weight.
- Model 2: 7-Day total for each nutrient vs. subsequent 14-day average weight.
- Model 3: 7-Day total for each nutrient vs. 7-day average weight starting 7 days later.
- Model 4: 1-Day total for each nutrient vs. weight the next day.
Let’s compute these features.
{ChatGPT loaded the dataframe here}
Step 3: Model Building
We will build both linear and non-linear models for each dataset.
Linear Models:
- Model 1: Linear regression with 7-day total nutrients vs. subsequent 7-day average weight.
- Model 2: Linear regression with 7-day total nutrients vs. subsequent 14-day average weight.
- Model 3: Linear regression with 7-day total nutrients vs. 7-day average weight starting 7 days later.
- Model 4: Linear regression with 1-day nutrients vs. weight the next day.
Non-Linear Models:
- We can use Random Forest Regressor as an example of a non-linear model.
- Perform cross-validation to avoid overfitting.
Let’s start by building the linear models and evaluating their performance. Then, we will proceed with the non-linear models.
| Model | MSE | R² | Intercept | Net Carbohydrates (g) | Sugar (g) | Fat (g) | Fiber (g) | Protein (g) |
| Model 1 | 17.500 | 0.522 | 198.207 | 0.005 | 0.018 | -0.021 | -0.109 | 0.030 |
| Model 2 | 17.022 | 0.527 | 198.250 | 0.004 | 0.016 | -0.018 | -0.107 | 0.029 |
| Model 3 | 18.061 | 0.502 | 198.082 | 0.004 | 0.018 | -0.020 | -0.109 | 0.029 |
| Model 4 | 39.691 | 0.130 | 204.767 | 0.007 | 0.020 | -0.055 | -0.208 | 0.050 |
Step 4: Non-Linear Model Building
We will now build non-linear models using Random Forest Regressor and evaluate their performance.
Random Forest Regressor
- A robust and versatile non-linear model.
- Perform cross-validation to avoid overfitting and ensure model reliability.
Let’s proceed with training and evaluating Random Forest models for each dataset.
| Model | MSE | R² |
| Model 1 | 53.32 | -7.22 |
| Model 2 | 47.57 | -7.18 |
| Model 3 | 51.96 | -6.96 |
| Model 4 | 68.09 | -8.23 |
Summary of Results
The linear models showed relatively better performance compared to the non-linear Random Forest models. Here’s a summary of the model evaluations (RF = random forest}:
| Nutrient/Metric | Model 1 (Linear) | Model 2 (Linear) | Model 3 (Linear) | Model 4 (Linear) | Model 1 (RF) | Model 2 (RF) | Model 3 (RF) | Model 4 (RF) |
|---|---|---|---|---|---|---|---|---|
| Net Carbohydrates | 0.004707 | 0.003693 | 0.004344 | 0.006977 | – | – | – | – |
| Sugar | 0.017555 | 0.015926 | 0.017708 | 0.019937 | – | – | – | – |
| Fat | -0.021072 | -0.018234 | -0.020224 | -0.054639 | – | – | – | – |
| Fiber | -0.108539 | -0.106878 | -0.109477 | -0.207999 | – | – | – | – |
| Protein | 0.029510 | 0.028574 | 0.029292 | 0.050099 | – | – | – | – |
| MSE | 17.50 | 17.02 | 18.06 | 39.69 | 53.32 | 47.57 | 51.96 | 68.09 |
| R² | 0.52 | 0.53 | 0.50 | 0.13 | -7.22 | -7.18 | -6.96 | -8.23 |
Recommendations and Justifications
- Linear Models Outperform Random Forest: The linear models consistently showed better performance with lower MSE and higher R² scores. This suggests that the relationship between the nutritional intake and weight might be better captured by a linear relationship rather than a complex non-linear model.
- Model 2 as the Best Model: Among the linear models, Model 2 showed the best performance with the lowest MSE (17.02) and the highest R² (0.53). This model uses a 7-day total for each nutrient to predict the subsequent 14-day average weight, providing a balanced approach to account for delayed effects of nutrition on weight.
- Impact of Individual Nutrients: From the linear model coefficients, we can infer:
- Net Carbohydrates: Positive impact on weight.
- Sugar: Positive impact on weight.
- Fat: Negative impact on weight.
- Fiber: Negative impact on weight.
- Protein: Positive impact on weight.
Visualizations
Let’s create visualizations to show the impact of each nutrient on weight as per the best linear model (Model 2). {The y-axis, the vertical, is the value of the coefficient for the linear model; the x-axis is the nutrient}
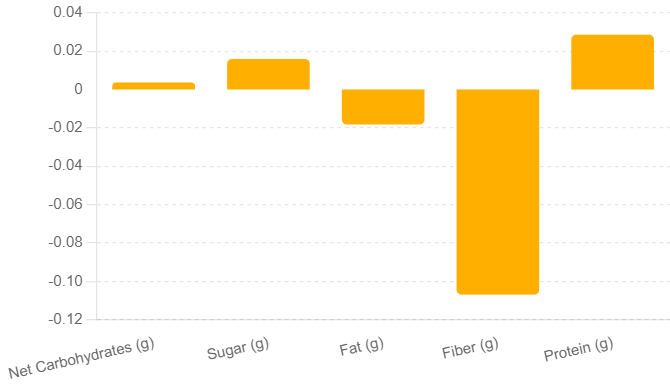
{Numerical labels removed – don’t worry about how much I weigh = smile=}
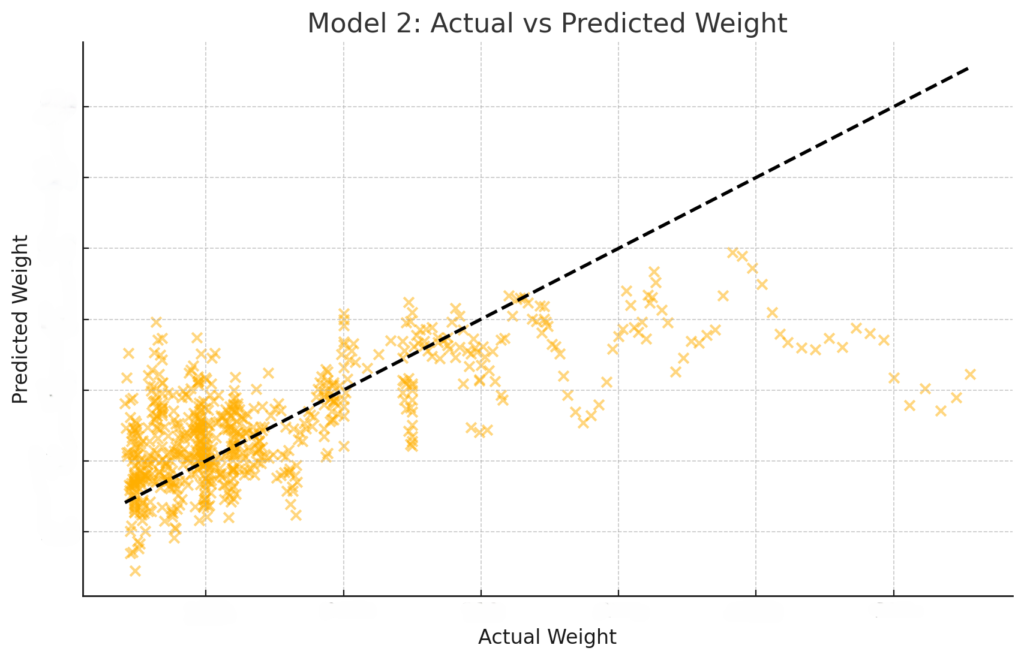
Improving the Model By Truncating the Data
ChatGPT Prompt: I noticed the model gets worse the higher the actual weight. Since weight declined over the analysis timeframe, how can I improve the model? In addition to your recommendations, try rerunning the linear models starting with April 5, 2022 where the weight first hit xxx pounds.
Improved Model Results
The results from the filtered data starting from April 5, 2022, where the weight first hit xxx pounds, show improved performance, especially for the linear models.
| Model | Description | MSE | R² |
|---|---|---|---|
| Model 1 | 7-Day Total Nutrients vs. Subsequent 7-Day Average Weight | 8.68 | 0.47 |
| Model 2 | 7-Day Total Nutrients vs. Subsequent 14-Day Average Weight | 7.99 | 0.49 |
| Model 3 | 7-Day Total Nutrients vs. 7-Day Average Weight Starting 7 Days Later | 8.95 | 0.46 |
| Model 4 | 1-Day Nutrients vs. Weight the Next Day | 15.78 | 0.10 |
Analysis and Recommendations
- Improvement with Filtering: The models show lower Mean Squared Error (MSE) and higher R² values after filtering the data starting from April 5, 2022. This suggests that the model’s accuracy improved when focusing on a more consistent timeframe where weight was declining.
- Best Model: Model 2 remains the best model, with the lowest MSE (7.99) and the highest R² (0.49).
Visualizations
Let’s update the graphs to show actual versus predicted weights for the linear models using the filtered data.
{numerical labels removed, best graph retained and others removed for brevity}
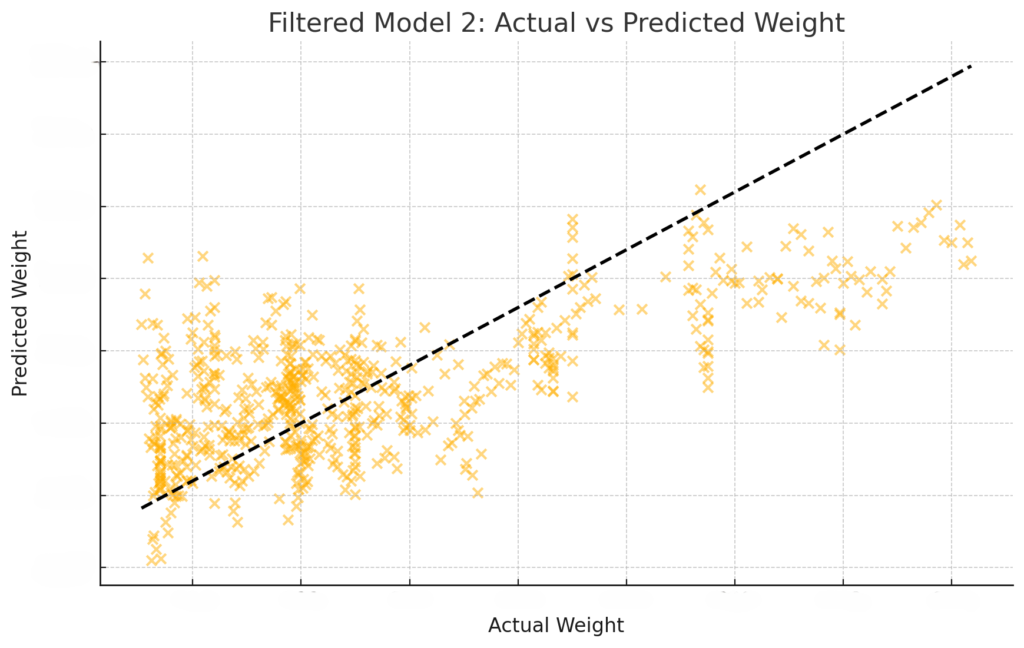
Conclusion
- Filtering the Data: Starting from April 5, 2022, significantly improved the model’s performance. This period captures more consistent weight trends.
- Best Model: Model 2, using 7-day total nutrients to predict subsequent 14-day average weight, remains the best model.
- Visual Analysis: The scatter plots show that the predictions are closer to the actual values, particularly for models 1, 2, and 3, indicating better model performance.
These steps help in refining the model’s predictive power, especially by focusing on a consistent timeframe.
Final Thoughts
Overall, I was encouraged to see consistent conclusions from different analyses of my nutrient and weight data. Given the truncated, or filtered, model produced the same disaggregated conclusions as the full data model, I am curious to see how these results will hold up after I lose more weight. I will not use these models to predict my weight (and I do not have a use case for such predictions), but I am relatively confident that the coefficients of the linear regression (Model 2) provide good, directional guidance for my diet.
The results made me wonder whether the negative impact on weight by fat came from a satiation effect. I tried to tease out some insights by manually graphing fat versus calories. I overlayed various trendlines, balancing simplicity, overfitting, and R². A logarithmic fit tells the story of slower growth in calorie consumption as the amount of fat increases. This is essentially a crowding out of other calorie-generating nutrients, presumably sugar, that would contribute to weight gain. Note that a linear fit and an exponential produced R² values close to the logarithmic fit.
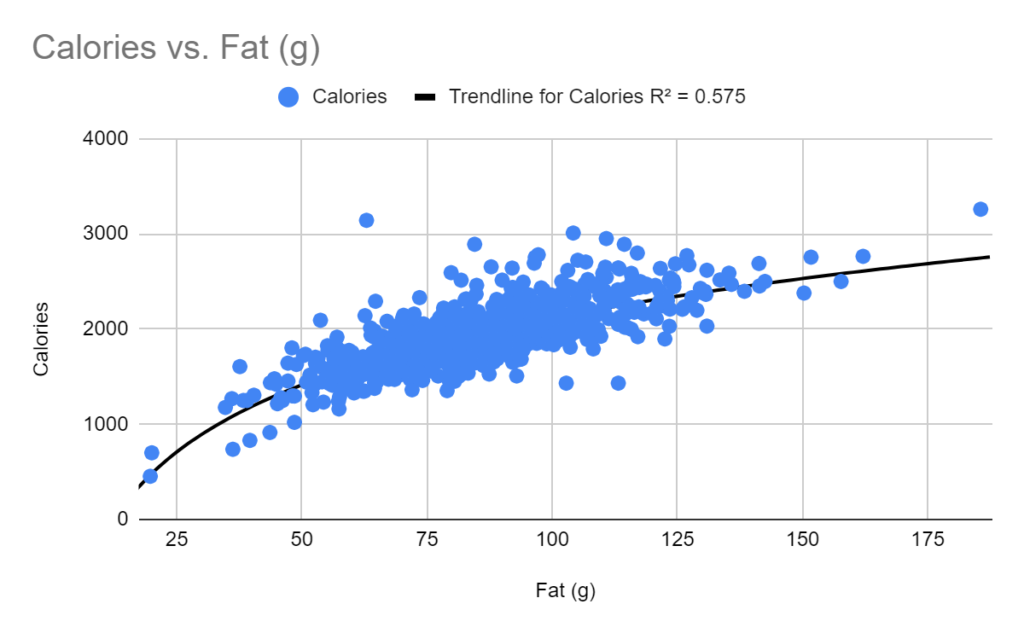
While this graph tells a good story, I will need more data and more careful measurements to produce a conclusive outcome. Still, like the coefficients on the linear model, the story makes directional sense.
For comparison, I tried a similar graph of fiber versus calories. I expected to see an even stronger satiation effect from fiber. I was surprised to see essentially no relationship. I overlayed a logarithmic curve for comparative purposes.
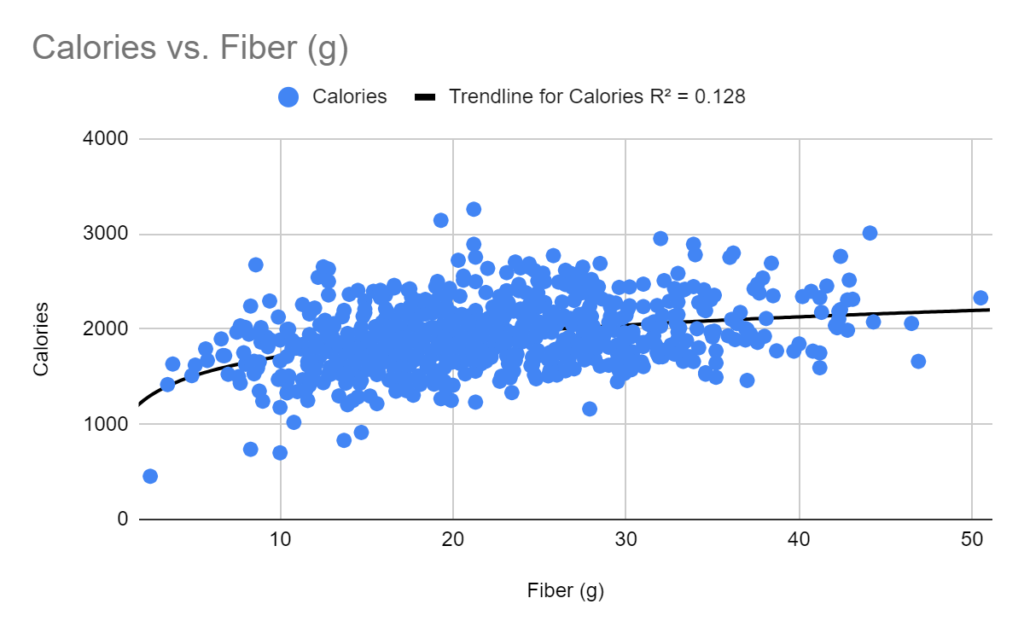
This graph leaves me wondering about the mechanism that drives the weight loss from fiber intake. To understand better, I will need to examine more closely the foods I eat with the highest fiber and even examine the timing of my highest fiber days.
I would also like to more rigorously confirm my assumption that protein contributes to weight gain through muscle. This conclusion certainly fits the physiological mechanism for metabolizing protein, but it also ignores the possibility that I am consuming a lot more protein than my body needs (for more research on the body’s potential to convert protein into glucose see “A high-protein diet for reducing body fat: mechanisms and possible caveats” from the National Institute of Health). My average daily protein intake over this timeframe was 104g. The Mayo clinic advises that 10-35% of calories should come from protein with physically active and older folks pushing toward higher needs. My current target generates 30% of calories from protein.
Finally, it could be worth incorporating my exercise activity in the analysis. Currently, I use a setting in MyFitnessPal that reduces sugar and carbohydrates based on the number of calories burned in exercise. In future work, I could use gross carbs and sugar levels and represent exercise as amount of calories burned in a given week. Still, my intuition tells me the relative, directional conclusions will remain the same.
Regardless, the analysis of these results have made me even more diligent about reducing sugar consumption. I started the weight loss journey knowing I needed to get my blood sugar levels down, and I accomplished the first phase of my goals thanks to tracking my diet in MyFitnessPal. I am looking forward to gaining more sophisticated insights on how my diet interacts with my metabolism.
ChatGPT Data Analysis was a very convenient tool for conducting this analysis. Bugs and crashes aside, it shows promise for providing a starting point for many types of analyses. I particularly like ChatGPT’s ability to choose and assess models specific to a given dataset and analytic objective.
I would love to hear from you in the comments below. If you have any feedback on this analysis or want to share your own quantitative analyses on weight loss, let me know.
Appendix
To complete the educational experience, I asked ChaptGPT to examine its work. I truncated the response to the following prompt to eliminate redundancy with the results already presented above.
ChatGPT Prompt: “Explain in detail the statistical principles involved in this analysis. Justify your choice of models.”
Detailed Explanation of Statistical Principles
Linear Regression
Principles:
- Linear regression models the relationship between a dependent variable (weight) and one or more independent variables (nutrients) by fitting a linear equation to observed data.
- The equation of a simple linear regression is 𝑦 = β0 + β1x, where y is the dependent variable, x is the independent variable, and β0 and β1 are coefficients.
- In multiple linear regression (used here), the model extends to 𝑦=𝛽0+𝛽1𝑥1+𝛽2𝑥2+…+𝛽𝑛𝑥𝑛, where x1,x2,…,xn are the independent variables (nutrients).
Justification:
- Linear regression is straightforward and interpretable. The coefficients directly indicate the impact of each nutrient on weight.
- Linear regression assumes a linear relationship, which, based on exploratory analysis, appears reasonable for this dataset.
Evaluation Metrics:
- Mean Squared Error (MSE): Measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. Lower MSE indicates a better fit.
- R² (Coefficient of Determination): Indicates the proportion of the variance in the dependent variable that is predictable from the independent variables. Higher R² indicates a better fit.
2. Model Selection and Lags
Principles:
- Time series data often exhibit dependencies that span multiple periods. Thus, considering lagged variables can capture delayed effects of nutrients on weight.
- Different models explore various lag structures to determine the most effective way to predict weight based on past nutrient intake.
Justification:
- Model 1: 7-Day Total Nutrients vs. Subsequent 7-Day Average Weight
- This model considers the immediate effect of a week’s nutrient intake on the subsequent week’s average weight, capturing short-term effects.
- Model 2: 7-Day Total Nutrients vs. Subsequent 14-Day Average Weight
- This model examines the impact of nutrient intake over a week on weight over the following two weeks, accounting for delayed physiological effects.
- Model 3: 7-Day Total Nutrients vs. 7-Day Average Weight Starting 7 Days Later
- This model looks at the effect of a week’s nutrient intake with a one-week delay, separating the intake period and the effect period.
- Model 4: 1-Day Nutrients vs. Weight the Next Day
- This model provides a baseline by considering the immediate next-day effect of daily nutrient intake.
3. Data Filtering and Analysis Period
Principles:
- Data consistency and homogeneity can significantly impact model performance. Filtering data to a more consistent period can improve model accuracy.
Justification:
- Weight fluctuations over time can introduce noise. By focusing on a period with more consistent weight trends (starting from April 5, 2022, when the weight was more stable), we improve the model’s ability to capture genuine relationships between nutrients and weight.
